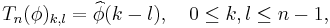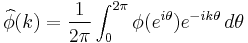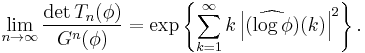Szegő limit theorems

In mathematical analysis, the Szegő limit theorems describe the asymptotic behaviour of the determinants of large Toeplitz matrices.[1][2] They were first proved by Gábor Szegő.

Contents

Notation

Let φ : T→C be a complex function ("symbol") on the unit circle. Consider the n×n Toeplitz matrices Tn(φ), defined by

T_n(\phi)_{k,l} = \widehat\phi(k-l), \quad 0 \leq k,l \leq n-1,

where

\widehat\phi(k) = \frac{1}{2\pi} \int_0^{2\pi} \phi(e^{i\theta}) e^{-ik\theta} \, d\theta

are the Fourier coefficients of φ.

First Szegő theorem

The first Szegő theorem[1][3] states that, if φ > 0 and φ ∈ L1(T), then

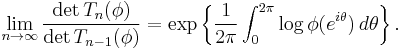
\lim_{n \to \infty} \frac{\det T_n(\phi)}{\det T_{n-1}(\phi)} = \exp \left\{ \frac{1}{2\pi} \int_0^{2\pi} \log \phi(e^{i\theta}) \, d\theta \right\}.

 

 

 

 

(1)

The right-hand side of (1) is the geometric mean of φ (well-defined by the arithmetic-geometric mean inequality); denote it G(φ).

Second Szegő theorem

The second (or strong) Szegő theorem[1][4] asserts that if, in addition, the derivative of φ is Hölder continuous of order α > 0, then

\lim_{n \to \infty} \frac{\det T_n(\phi)}{G^n(\phi)} = \exp \left\{ \sum_{k=1}^\infty k \left| \widehat{(\log \phi)}(k)\right|^2 \right\}.

References

  1. ^ a b c Böttcher, Albrecht; Silbermann, Bernd (1990). "Toeplitz determinants". Analysis of Toeplitz operators. Berlin: Springer-Verlag. p. 525. ISBN 3-540-52147-X. MR1071374. 
  2. ^ Ehrhardt, T.; Silbermann, B. (2001), "Szegő limit theorems", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=Szegö_limit_theorems 
  3. ^ Szegő, G. (1915). "Ein Grenzwertsatz über die Toeplitzschen Determinanten einer reellen positiven Funktion". Math. Ann. 76: 490–503. 
  4. ^ Szegő, G. (1952). "On certain Hermitian forms associated with the Fourier series of a positive function.". Comm. Sém. Math. Univ. Lund [Medd. Lunds Univ. Mat. Sem.]: 228–238. MR0051961.